상세 컨텐츠
본문
건설공사에서는 많은 불확실성이 존재하지만 기존의 CPM기법은 이러한 불확실성을 반영하지 못하고 확정적인 시간으로 계산합니다. CPM의 이런 단점을 개선하기 위해 개발된 것이 PERT기법입니다. 여기서는 PERT기법에 대해 살펴보겠습니다.
PERT기법
PERT(Program Evaluation and Review Technique)는 1950년대에 미해군에서 개발한 것으로 작업일정 및 공사기간을 결정하고 주공정선을 구하는 방법은 CPM기법과 유사합니다.
그런데 PERT기법은 작업시간을 추정할 때 확률적인 기법을 사용하여 세가지 시간 추정치의 가중평균으로서 작업기간에 대한 기대치를 계산합니다.
- 낙관시간치(Optimistic duration; to) : 가장 바람직한 환경 조건에서 작업을 수행하는 데 필요한 추정시간. 상대적으로 가장 짧은 시간. 이 시간보다 단축될 확률은 0이다.
- 비관시간치(Pessimistic duration; tp) : 가장 불리한 환경 조건에서 작업을 수행하는 데 필요한 추정시간. 상대적으로 가장 긴 시간. 이 시간보다 단축되거나 같을 확률은 100%이다.
- 개연시간치(Most likely duration; tm) : 실제 소요기간에 가장 가까운 추정시간. 낙관시간치와 비관시간치 사이에 위치한다.
예를 들어 우리가 어떤 작업이 얼마나 걸릴까를 추정할 때, 비슷한 작업의 과거 경험을 기초로 그 작업을 완수하는데 가능한 시간을 8일이라 추정할 수 있습니다. 그리고 만약 다른 문제가 없이 수월하게 작업이 직행된다면 5일 내에 끝마칠 수도 있으며, 만일 문제가 생기면 17일까지 걸릴 수 있다고 추정할 수도 있습니다.
이 때 8일은 개연시간치가 되고, 5일은 낙관시간치, 17일은 비관시간치가 됩니다. 이 때 작업기간은 세 가지 추정치로 기반으로 베타분포를 따른다고 가정합니다.
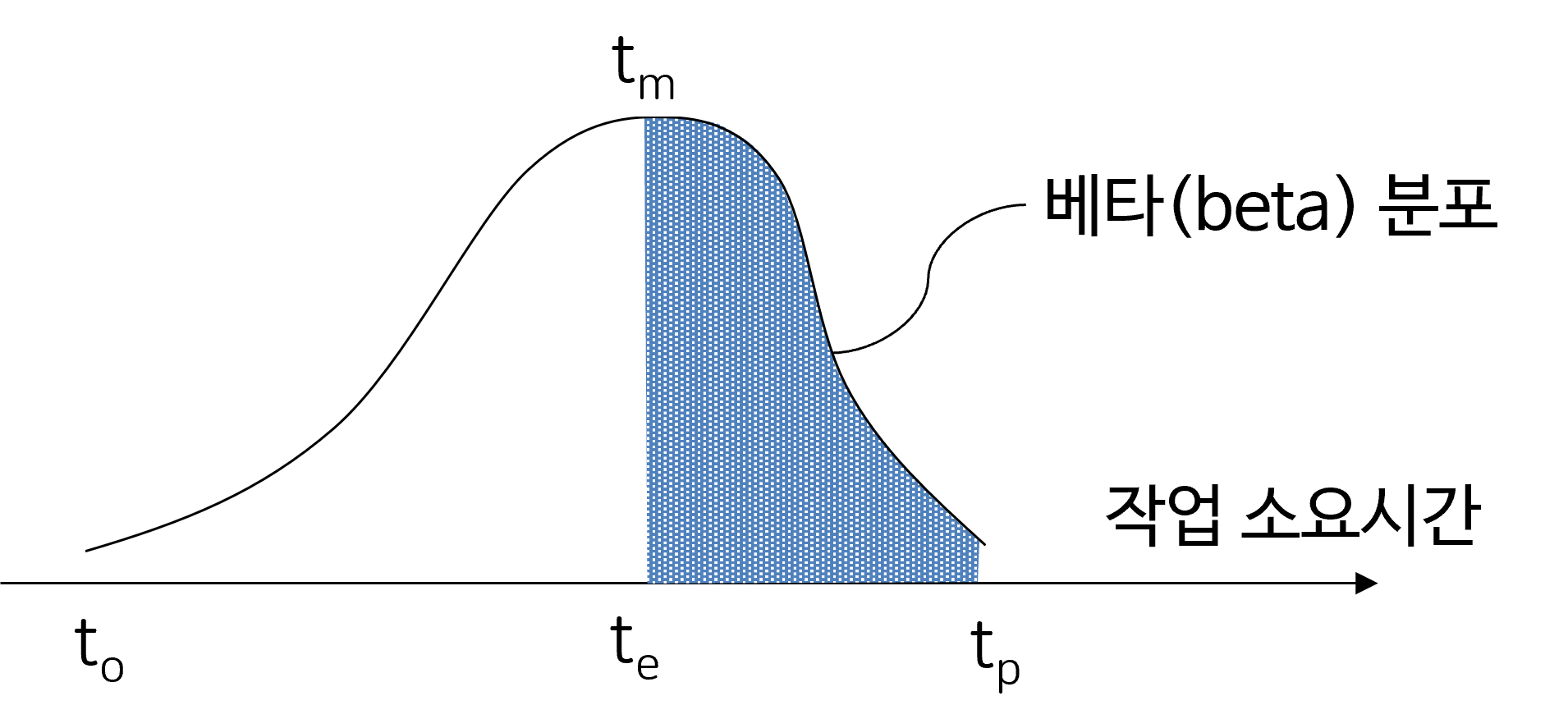
기대값과 분산
그런데 주공정선(CP)를 결정하고 전체 공기를 계산하기 위해서는 각 작업마다 하나의 값으로 계산해야만 합니다. 이렇게 3가지 추정값으로는 CPM을 이용하여 프로젝트의 전체 소요시간을 분석할 수 없기 때문에 개별 작업의 기대값(Expected duration of activity)을 계산해야만 합니다. 이 때 개별작업의 기대값은 다음과 같이 계산합니다.

이 값은 개연적시간에 가중치를 부여한 일종의 가중평균값인데, 베타분포의 양쪽 면적을 똑같이 분할하는 평균에 해당하는 값입니다. 따라서 기대값보다 작거나 클 확률이 모두 50%이 됩니다.
PERT에서는 기대값과 함께 분산도 사용합니다. 예를 들어 3가지 기대값이 다음과 같다고 가정하겠습니다.

위 표에서 보면 위쪽에 있는 추정치의 경우 비관치와 낙관치의 차이가 크지만, 아래쪽의 경우에는 상대적으로 작습니다. 따라서 개연치인 9일에 완료될 확률이 높다고 할 수 있습니다. 이처럼 각 작업의 소요시간의 불확실성의 정도를 나타내기 위해 분산(Estimated variance of the duration)을 사용하며 분산은 다음과 같이 계산합니다.
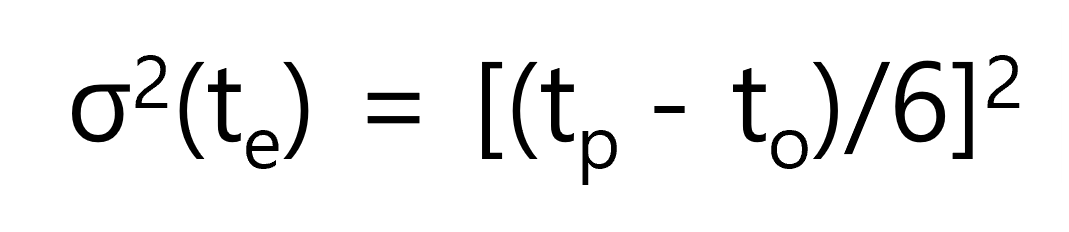
위 표에 있는 값을 대상으로 분산을 계산하면 다음과 같습니다. 계산결과를 보면 기대치는 모두 9일로 동일하지만 분산은 아래쪽이 0.11로 상대적으로 작은 것을 알 수 있습니다. 이렇게 분산을 이용하여 추정의 신뢰도를 확률적으로 계산할 수 있습니다.

PERT 예제
다음과 같은 프로젝트가 있을 때 PERT기법을 사용하여 일정을 계산해 보겠습니다 .
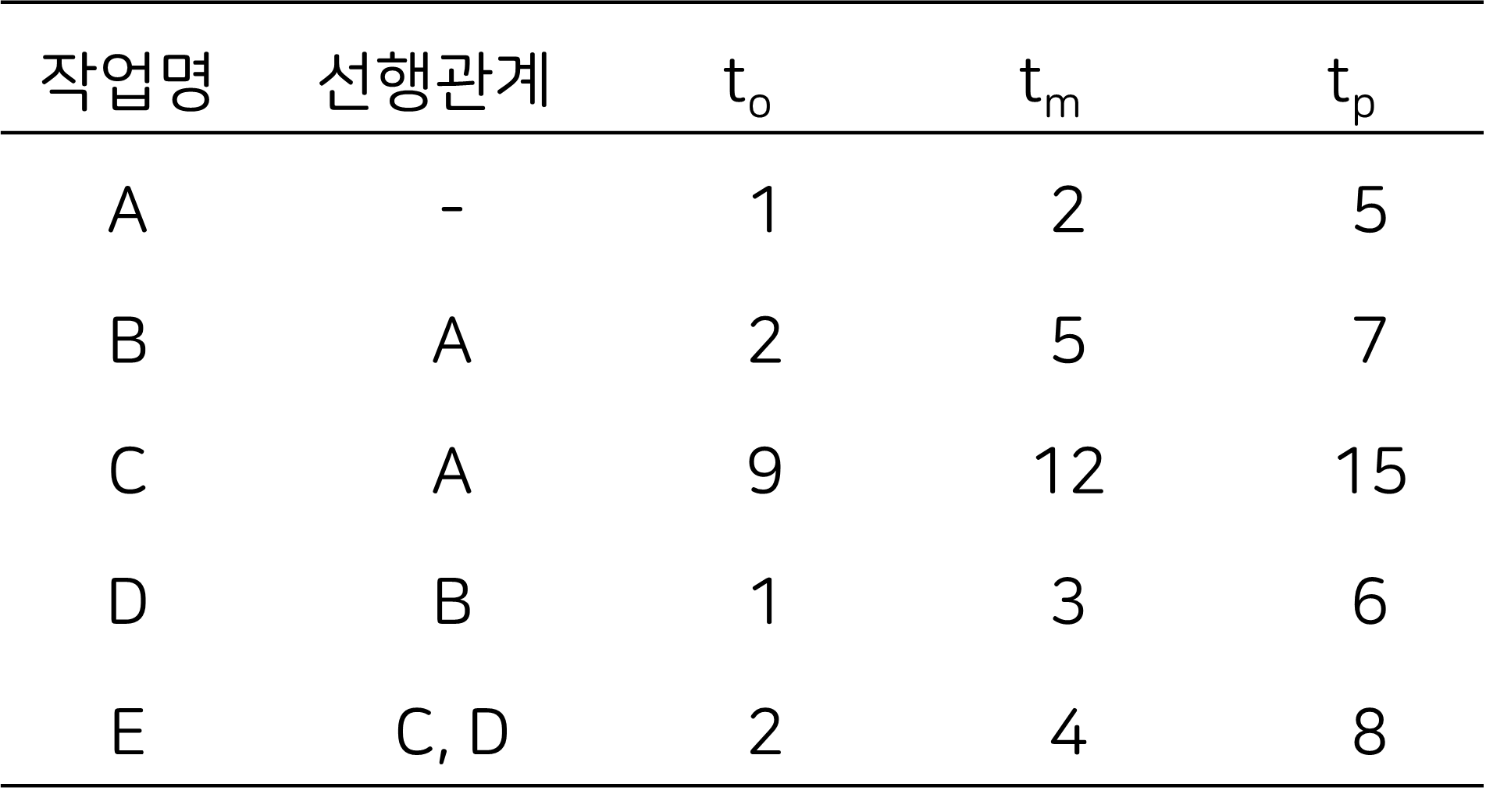
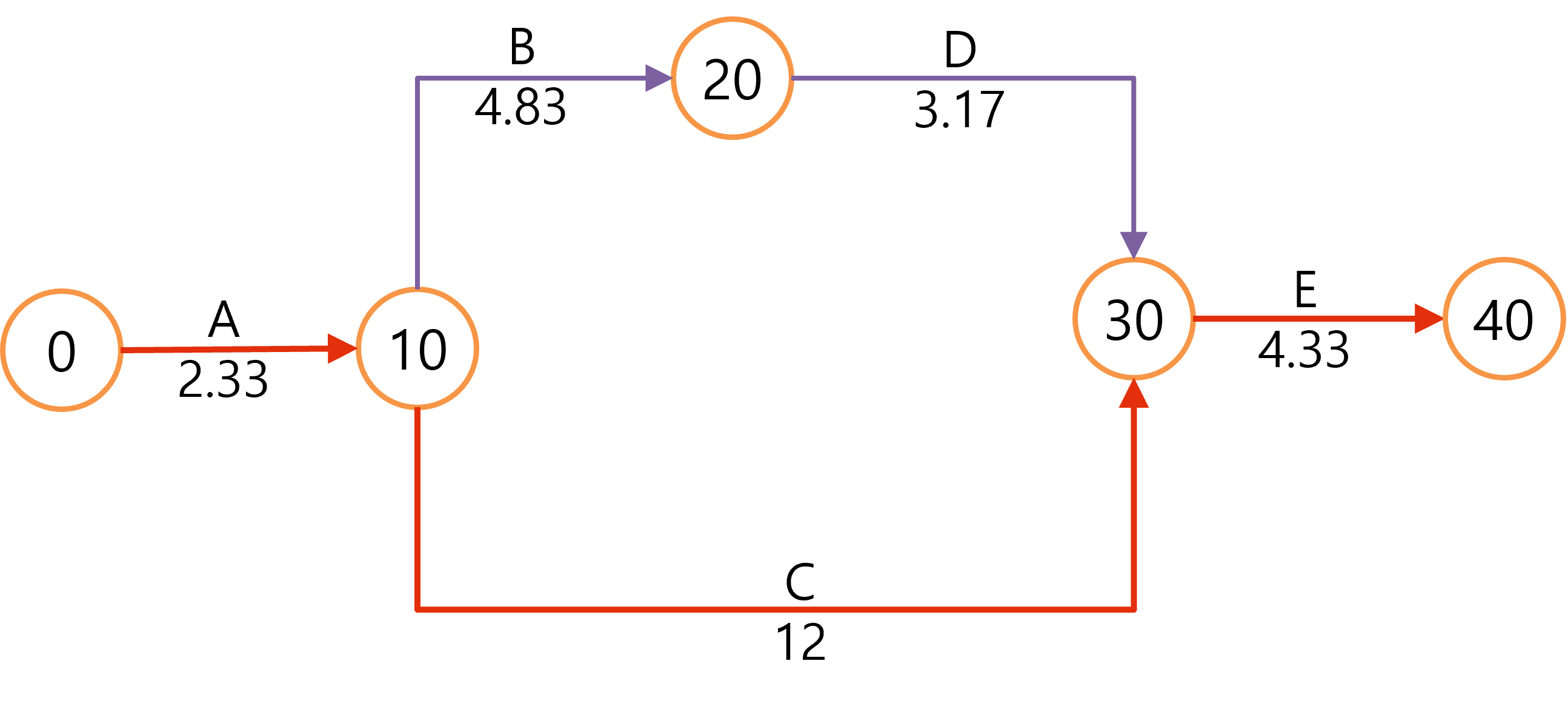
작업의 선행 관계에 따라 ADM으로 그리면 다음과 같습니다.
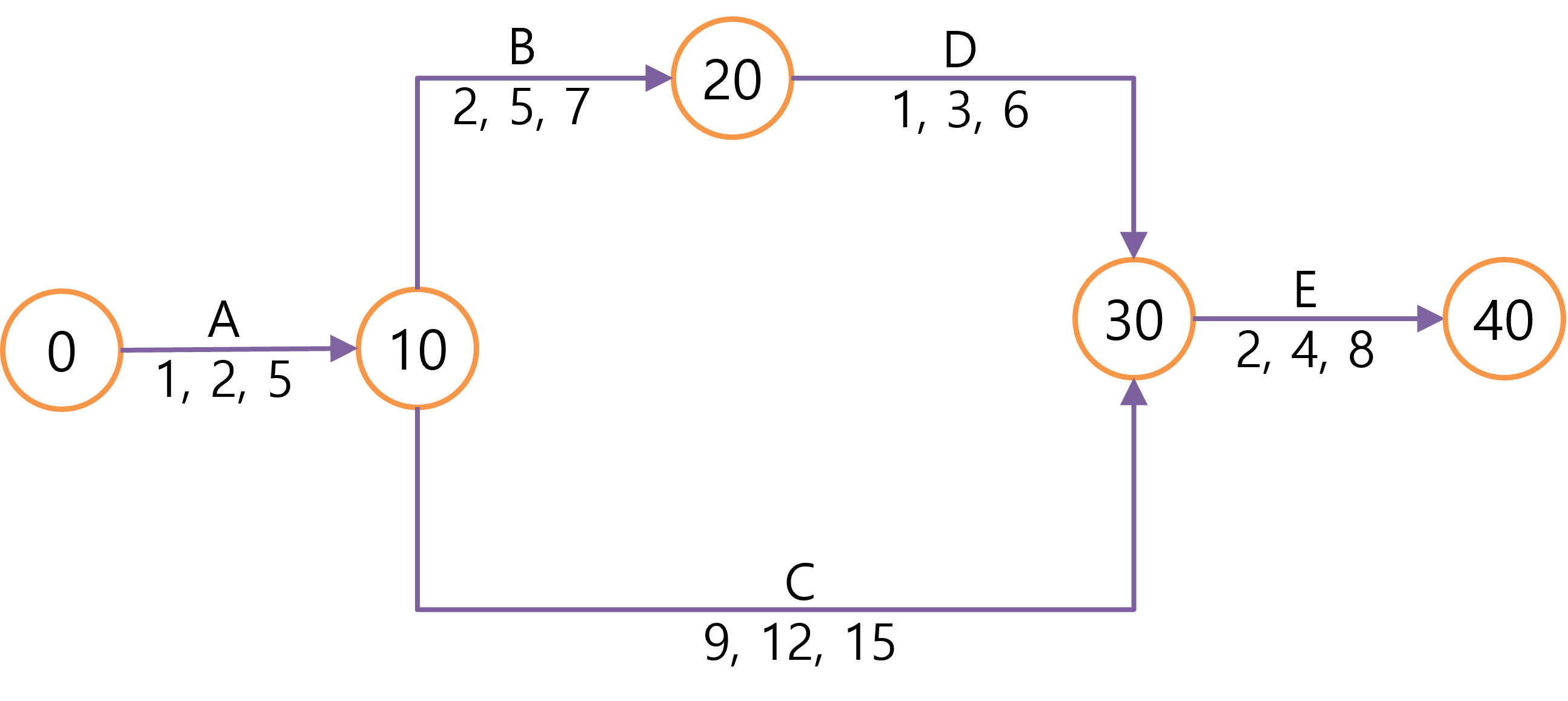
먼저 각 작업의 기대치와 분산을 다음 그림과 같이 계산합니다.

모든 작업에 대해 기대값과 분산을 계산하면 다음과 같습니다.

각 작업의 기대값을 바탕으로 CPM 기법으로 전체 소요시간과 주공정선, 여유시간을 산출할 수 있습니다. 주공정선 A-C-E가 되고 총 공기 = 18.7일이 됩니다.
그럼 전체 프로젝트의 완수가능성은 어떻게 될까요? 이 완수가능성을 계산하려면 주공정선의 합계와 분산이 필요합니다. 각각 다음과 같이 계산할 수 있습니다.


앞의 프로젝트에 대입하면 결과는 다음과 같이 됩니다.
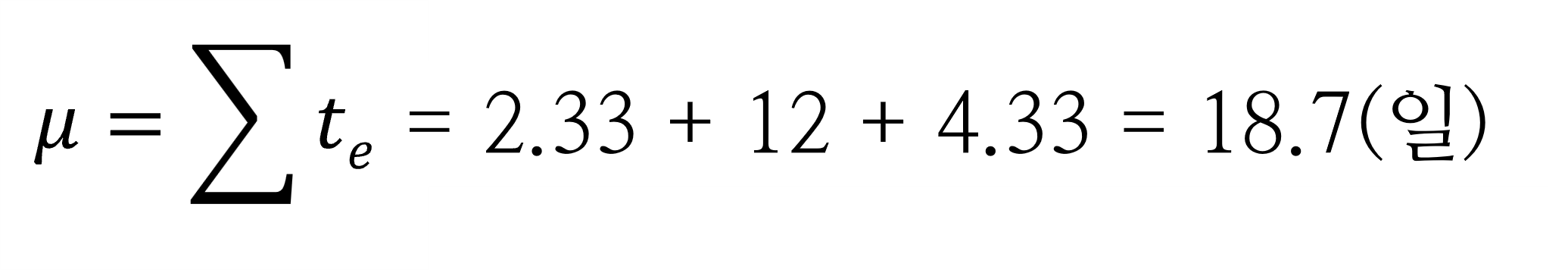
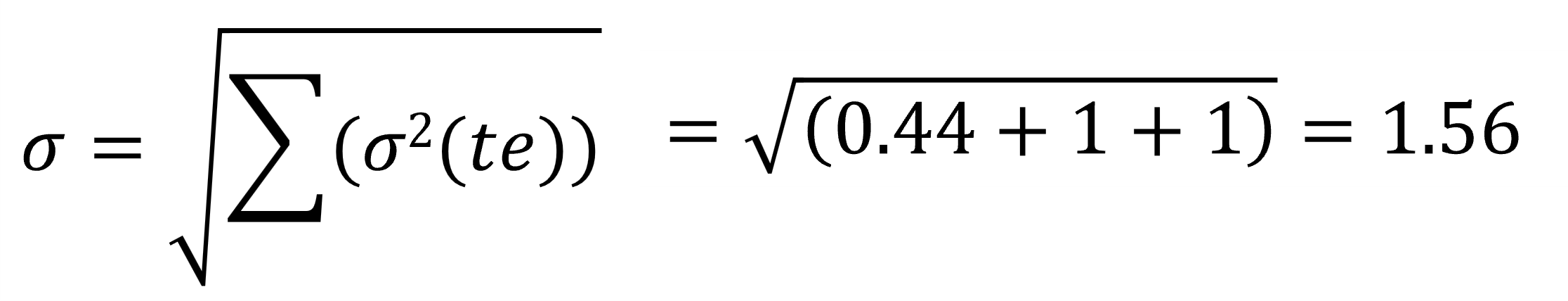
이렇게 평균과 기대값 가지고 완수확률을 계산할 수 있습니다. 각각의 작업은 베타분포를 따르지만 전체 작업을 합한 프로젝트 전체 소요시간은 정리에 따라 정규분포를 따르게 됩니다. 따라서 정규분포를 이용하여 완수 확률을 계산할 수 있습니다.
자 그럼 위 프로젝트를 16일 이전에 끝낼 수 있는 확률은 어떻게 될까요? 평균이 18.7이고 분산이 1.56이니 확률이 작을 것이라고 예상할 수 있습니다.
위에서 계산한 평균과 분산을 가지고 정규분포의 Z값을 구하면 다음과 같이 됩니다. Td는 목표 공기이므로 16입니다


이제 확률밀도함수에서 - 1.73보다 작은 확률값을 구하면 됩니다
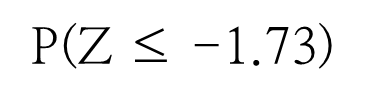
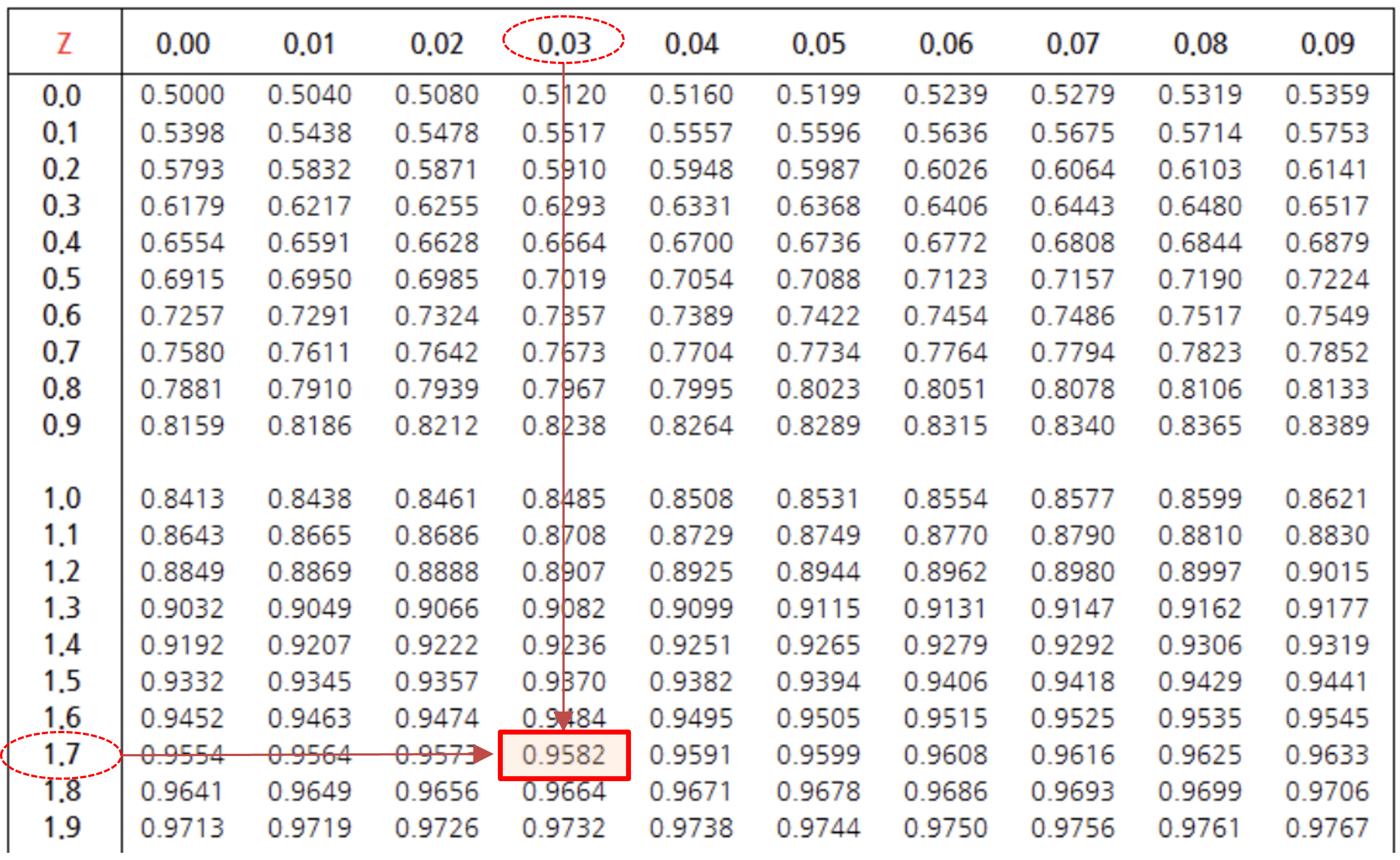
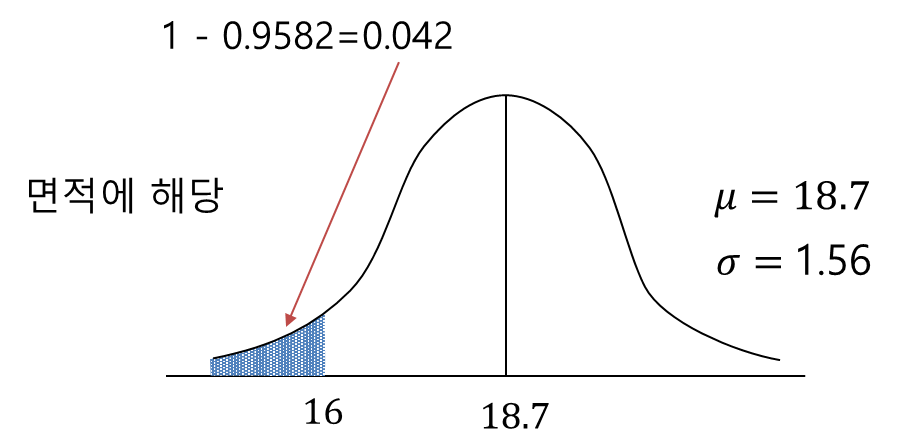
이 값은 결국 0.042에 해당합니다. 16일 이내에 끝낼 확률은 4.2%밖에 되지 않아 확률적으로 매우 어렵다는 것을 알 수 있습니다.
'공정관리 > 일정계산' 카테고리의 다른 글
| 작업의 여유시간(Float) 계산 - ADM기법 (0) | 2023.09.23 |
|---|---|
| 작업의 여유시간(Float) 계산 - PDM기법 (0) | 2023.09.23 |
| 일정계산(ADM) - CPM (0) | 2023.09.23 |
| 일정계산 - PDM (1) | 2023.09.20 |





